Mã hóa RSA là một hệ thống giải quyết những gì đã từng là một trong những vấn đề lớn nhất trong bảo mật: Làm thế nào có thể gửi cho ai đó một tin nhắn được mã hóa mà không có cơ hội chia sẻ mã trước đó? Bài viết này sẽ hướng dẫn cho bạn biết mã hóa RSA là gì, cách nó được phát triển và hoạt động cũng như một số vấn đề bảo mật mà nó phải đối mặt.

RSA là gì?

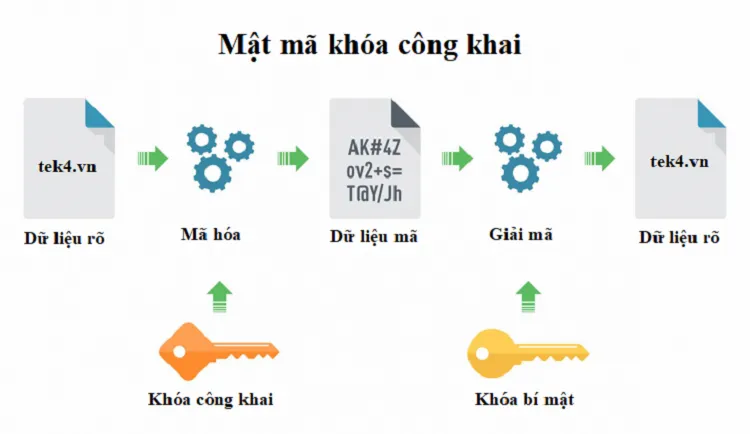
RSA là một hệ mã hóa bất đối xứng (asymmetric cryptography) sử dụng hai khóa khác nhau để mã hóa và giải mã. Public key (khóa công khai) được chia sẻ với bất kỳ ai và dùng để mã hóa thông tin, trong khi private key (khóa bí mật) được giữ kín và chỉ người sở hữu nó mới có thể giải mã thông tin. Bằng cách sử dụng public key, bất kỳ ai cũng có thể gửi thông tin một cách an toàn, nhưng chỉ người giữ private key mới có thể đọc được thông điệp. Điều này mang lại mức độ bảo mật cao vì dù thông tin có bị chặn, chỉ người có private key mới có thể giải mã.

 

Dù trên lý thuyết RSA có độ bảo mật rất cao, trong thực tế không có phương pháp nào đảm bảo an toàn tuyệt đối. Với sự phát triển của công nghệ như AI, máy tính lượng tử và siêu máy tính,… các hệ thống mã hóa hiện tại có thể trở nên dễ bị phá vỡ hơn. Hiện tại, các thuật toán khóa như RSA vẫn bảo vệ được thông tin trước các kỹ thuật tấn công thông thường, đặc biệt khi sử dụng máy tính cá nhân, nhưng trong tương lai có thể bị đe dọa bởi các công nghệ tiên tiến hơn.

Ứng dụng RSA

Nhìn chung, RSA đã mở ra kỷ nguyên mới cho chữ ký số, mang lại sự an toàn và đáng tin cậy cho giao tiếp và giao dịch trong thế giới kỹ thuật số. Dưới đây là một số ứng dụng RSA ở thời điểm hiện tại, theo dõi chi tiết bên dưới.

Chữ ký số

RSA là thuật toán tiên phong trong việc tạo ra chữ ký số, đánh dấu cột mốc quan trọng trong lĩnh vực bảo mật và khoa học dữ liệu. Nhờ cơ chế mã hóa bất đối xứng, RSA không chỉ đảm bảo tính bảo mật mà còn giúp kiểm tra tính toàn vẹn của dữ liệu – một yếu tố quan trọng trong các giao dịch số.

Chữ ký số giống như chữ ký tay nhưng hoạt động trong môi trường điện tử và hiện nay đã trở thành công cụ không thể thiếu trong các hợp đồng và giao dịch trực tuyến. Dù ngày càng phổ biến, việc cài đặt và sử dụng chữ ký số vẫn còn nhiều thách thức, khiến việc triển khai thực tế còn nhiều bất cập, dù việc đảm bảo tính xác thực và bảo mật khá ổn định.

Bảo mật kết nối trên web, email, VPN và các ứng dụng chat

RSA thường được sử dụng để mã hóa nội dung trong các ứng dụng chat, giúp bảo vệ các cuộc trò chuyện cá nhân và dữ liệu nhạy cảm. Bằng cách sử dụng cặp khóa công khai và khóa riêng (public key và private key), RSA đảm bảo rằng chỉ những người có quyền truy cập vào khóa riêng mới có thể giải mã dữ liệu được mã hóa. Điều này giúp ngăn chặn việc nghe lén, đánh cắp thông tin trên đường truyền bởi các hacker, từ đó bảo vệ sự riêng tư và bảo mật của người dùng trong các môi trường giao tiếp số.

Giao thức TLS/SSL

Khác đôi chút với các ứng dụng phía trên RSA đóng vai trò trong việc thiết lập kênh truyền tải an toàn giữa máy chủ và client trong TLS/SSL. Tại đây, RSA được sử dụng để mã hóa quá trình trao đổi khóa, đảm bảo rằng dữ liệu truyền tải qua internet, chẳng hạn như thông tin đăng nhập, thanh toán hoặc dữ liệu cá nhân luôn được bảo mật tuyệt đối. Nhờ có RSA, người dùng có thể truy cập các trang web với giao thức HTTPS và có thể yên tâm trước các cuộc tấn công man-in-the-middle và các hành vi đánh cắp dữ liệu khác. RSA là một thành phần quan trọng giúp duy trì sự an toàn và bảo mật của các giao dịch trực tuyến thông qua TLS/SSL. 

 

Cơ chế hoạt động của RSA

Được mô tả lần đầu bởi Ron Rivest, Adi Shamir và Len Adleman vào 1977 tại Học viện Công nghệ Massachusetts (MIT). Hoạt động của RSA dựa trên 4 bước chính: sinh khóa, chia sẻ key, mã hóa và giải mã.

Quá trình sinh hóa

Việc tạo khóa trong RSA dựa trên việc tìm ra bộ ba số tự nhiên: e, d, và n, với yêu cầu rằng khi mã hóa và giải mã thông điệp m, công thức sau được thỏa mãn:

m^e mod n = m^d mod n

Một điểm quan trọng là private key d phải được bảo mật tuyệt đối. Ngay cả khi ai đó biết được e, n, hay thông điệp m, họ cũng không thể tính được d. Cụ thể, quá trình sinh khóa trong RSA gồm các bước như sau:

1. Chọn hai số nguyên tố lớn p và q: Đây là hai số bí mật mà chỉ người tạo khóa mới biết.
2. Tính giá trị n = p * q: Giá trị này sẽ được dùng làm modulus cho cả public key và private key.
3. Tính phi hàm Carmichael λ(n): Đây là một số giả nguyên tố được tính bằng cách lấy bội chung nhỏ nhất (BCNN) của λ(p) và λ(q), với λ(p) = p – 1 và λ(q) = q – 1. Giá trị λ(n) sẽ được giữ bí mật.
4. Chọn số tự nhiên e: Chọn một số e trong khoảng (1, λ(n)) sao cho ƯCLN(e, λ(n)) = 1, nghĩa là e và λ(n) nguyên tố cùng nhau. Số e sẽ được dùng để mã hóa thông điệp.
5. Tính số d: Tìm số d sao cho d * e ≡ 1 mod λ(n), hay nói cách khác, d là nghịch đảo modulo của e theo λ(n). Số d này sẽ được dùng để giải mã thông điệp.
6. Public key: Là bộ số (n, e), và có thể chia sẻ công khai.
7. Private key: Là bộ số (n, d), cần được giữ bí mật.

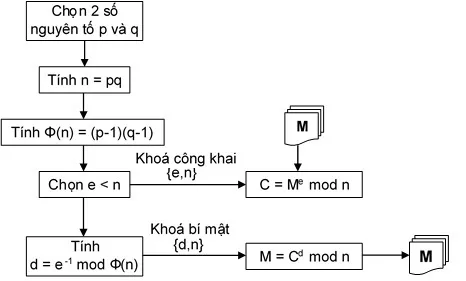
Để đảm bảo an toàn, cần bảo mật các số nguyên tố p và q, vì nếu chúng bị lộ, quá trình sinh khóa có thể bị phá vỡ.

 

Thực hành:

 

Trong thực tế, giá trị e thường được chọn là một số tương đối nhỏ để tăng tốc độ mã hóa và giải mã. Giá trị phổ biến nhất là e = 65537, vì nó đủ nhỏ để việc tính toán hiệu quả nhưng vẫn đảm bảo tính bảo mật.

 

Ngoài ra, có thể sử dụng phi hàm Euler φ(n) = (p – 1) * (q – 1) thay cho λ(n). Vì φ(n) là bội số của λ(n), nên số d được tính toán từ φ(n) vẫn sẽ đáp ứng điều kiện d * e ≡ 1 mod φ(n). Tuy nhiên, việc này có thể khiến giá trị d trở nên lớn hơn cần thiết trong một số trường hợp.

 

Mã hóa và giải mã trong RSA

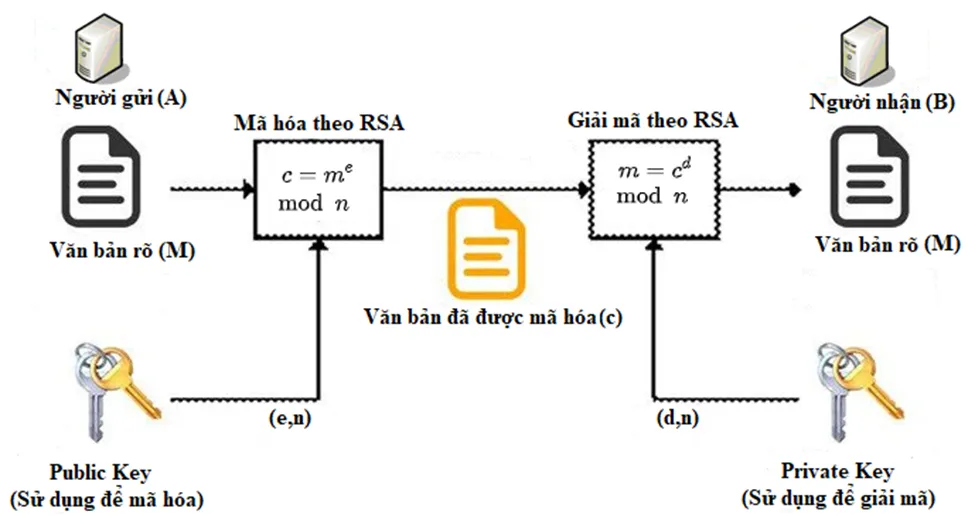
Trong quá trình mã hóa và giải mã bằng RSA, chúng ta sử dụng public key (n, e) để mã hóa và private key (n, d) để giải mã. Dưới đây là các bước chi tiết:

Mã hóa: Khi có một bản rõ (thông điệp) M, ta cần chuyển nó thành một số tự nhiên m sao cho 0 < m < n và m nguyên tố cùng nhau với n. Điều này có thể thực hiện dễ dàng bằng cách sử dụng các kỹ thuật padding (thêm dữ liệu bổ sung). Sau đó, ta tiến hành mã hóa số m thành c (bản mã) bằng công thức:

c = m^e mod n

Giá trị c sau đó sẽ được gửi tới người nhận.

Giải mã: Người nhận sử dụng private key (n, d) để giải mã bản mã c nhằm lấy lại số m bằng công thức:

m = c^d mod n

Sau khi có m, ta có thể khôi phục lại bản tin ban đầu M bằng cách đảo ngược quá trình padding.

 

Ví dụ

 

Giả sử: Chọn hai số nguyên tố p = 5 và q = 7, tính toán:

 

n = p * q = 35

 

φ(n) = (p-1)(q-1) = 4 * 6 = 24

 

Chọn e = 5 vì ƯCLN(5, 24) = 1, sau đó tính d = 29 vì:

 

d * e – 1 chia hết cho 24 (29 * 5 – 1 chia hết cho 24)

 

Giả sử thông điệp m = 32 (dấu cách), quá trình mã hóa và giải mã diễn ra như sau:

 

 

 

 

• Mã hóa: c = 32^5 mod 35 = 2
• Giải mã: m = 2^29 mod 35 = 32

 

Kết quả cuối cùng, m khớp với thông điệp ban đầu.

 

Cơ chế hoạt động chữ ký số

Chữ ký số dựa trên hệ mã hóa RSA hoạt động tương tự như quá trình mã hóa và giải mã thông tin. Tuy nhiên, vai trò của public key và private key trong chữ ký số có sự thay đổi:

• Tạo chữ ký: Người gửi sử dụng private key của mình để tạo ra chữ ký số.
• Xác thực chữ ký: Người nhận dùng public key của người gửi để xác thực tính hợp lệ của chữ ký.

Cách tạo và xác thực chữ ký số

Vì việc mã hóa toàn bộ bản tin có thể tốn thời gian và không hiệu quả, thay vì mã hóa cả bản tin, chỉ giá trị hash của bản tin được mã hóa. Phương pháp này có nhiều ưu điểm:

• Tính một chiều của hàm hash: Hàm hash là một hàm một chiều, do đó, ngay cả khi biết giá trị hash, cũng không thể khôi phục lại bản tin gốc.
• Độ dài cố định: Giá trị hash có độ dài cố định và nhỏ, giúp giảm dung lượng của chữ ký số.
• Kiểm tra tính toàn vẹn: Hash còn giúp kiểm tra xem bản tin có bị thay đổi trong quá trình truyền tải hay không. Nếu giá trị hash của bản tin không trùng khớp, nghĩa là dữ liệu đã bị thay đổi.

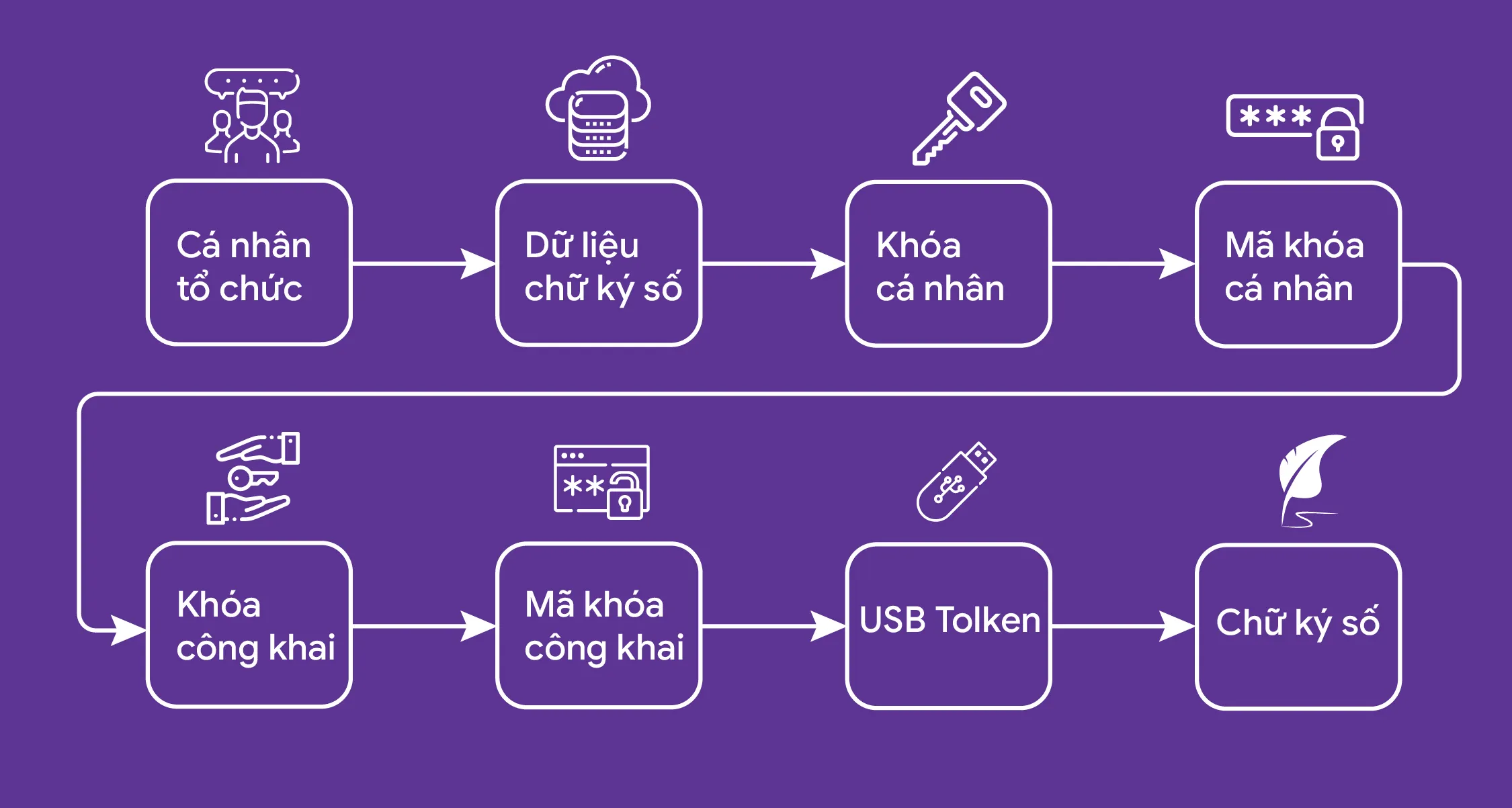
Lợi ích mà chữ ký số mang lại

• Xác định nguồn gốc: Với hệ mã hóa bất đối xứng, chỉ chủ sở hữu private key mới có thể tạo ra chữ ký số hợp lệ. Người nhận dùng public key để giải mã chữ ký và tính lại giá trị hash của bản tin. Nếu giá trị hash khớp với hash trong chữ ký số, chữ ký là hợp lệ và bản tin không bị thay đổi.
• Giữ nguyên tính toàn vẹn của dữ liệu: Chữ ký số đảm bảo rằng tin nhắn không thể bị chỉnh sửa. Nếu một kẻ tấn công thay đổi nội dung, giá trị hash sẽ khác, khiến việc xác thực chữ ký không thành công. Ngay cả khi kẻ tấn công biết giá trị hash và nội dung tin nhắn, hắn không thể thay đổi chữ ký số nếu không có private key.
• Không thể phủ nhận: Chữ ký số trong các giao dịch giúp xác định rõ nguồn gốc. Vì chỉ chủ sở hữu private key mới có thể tạo ra chữ ký, họ không thể phủ nhận rằng mình đã ký bản tin đó. Điều này giúp tăng tính pháp lý và trách nhiệm trong các giao dịch trực tuyến.

Rủi ro tiềm ẩn, thách thức về an ninh

Dù RSA là một hệ mã hóa mạnh mẽ, vẫn có những thách thức về an ninh, đặc biệt khi công nghệ tính toán phát triển mạnh mẽ. Tuy nhiên, chữ ký số dựa trên RSA vẫn là một phương thức bảo mật đáng tin cậy và phổ biến trong giao dịch và truyền tải dữ liệu hiện nay.

Các khái niệm cơ bản cần biết trong RSA

• Hàm trapdoor
• Tạo số nguyên tố
• Hàm phi Carmichael

Hàm trapdoor

Mã hóa RSA hoạt động dựa trên tiền đề rằng thuật toán dễ dàng tính toán theo một hướng. Nhưng hầu như không thể thực hiện ngược lại. Ví dụ nếu bạn được cho biết rằng 701,111 là tích của hai số nguyên tố, vậy bạn có thể tìm ra hai số đó là bao nhiêu không?

Ngay cả với máy tính hay PC thì hầu hết chúng ta cũng sẽ không biết bắt đầu từ đâu chứ đừng nói đến việc tìm ra câu trả lời. Nhưng nếu lật lại mọi thứ thì nó sẽ dễ dàng hơn rất nhiều. Kết quả của:

907 x 773

Nếu bạn dùng máy tính để tính phép toán này thì bạn sẽ phát hiện câu trả lời là 701,111 và nó đã được đề cập trước đó. 907 và 773 này là hai số nguyên tố cần trả lời cho câu hỏi đầu tiên của chúng tôi. Điều này cho chúng ta thấy rằng một số phương trình có thể dễ dàng giải ra một cách dễ dàng, nhưng ngược lại dường như không thể.

Một khía cạnh thú vị khác của phương trình này là việc tìm ra một trong các số nguyên tốt rất đơn giản nếu bạn đã có số còn lại. Nếu bạn cho biết rằng 701,111 là kết quả của 907 nhân với một số nguyên tố khác, bạn sẽ tìm ra được số nguyên tố đó với phương trình sau:

701,111 ÷ 907 = 773

Bởi vì điều này, RSA sử dụng số lượng lớn hơn nhiều. Kích thước của các số nguyên tố trong quá trình vận hành RSA là như nhau. Nhưng trong RSA 2048-bit, chúng sẽ kết hợp với nhau để tạo ra các key dài 617 chữ số. Để hình dung nó, một key sẽ là một số có kích thước như sau:

Copy

99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999

Tạo số nguyên tố

Các chức năng của hàm trapdoor đã được đề cập ở trên tạo cơ sở cho cách thức hoạt động của các lược đồ mã hóa public key và private key. Các thuộc tính của chúng cho phép chia sẻ public key mà không gây nguy hiểm cho tin nhắn hoặc tiết lộ private key. Chúng cũng cho phép dữ liệu được mã hóa bằng một key theo cách mà chỉ có thể giải mã bằng key khác.

Các số nguyên tố trong RSA cần phải rất lớn và cũng tương đối xa nhau. Các số nhỏ hoặc gần nhau sẽ dễ bị bẻ khóa hơn nhiều. Mặc dù vậy, ví dụ của chúng tôi sẽ sử dụng các số nhỏ hơn để làm cho mọi thứ dễ theo dõi và tính toán hơn.

Giả sử kiểm tra tính nguyên tố cho các số nguyên tố mà chúng ta đã sử dụng ở trên, 907 và 773. Bước tiếp theo là khám phá module (n), sử dụng công thức sau:

n = p x q

Với p = 907 and q = 773

Nên:

• n = 907 x 773
• n = 701,111

Hàm phi Carmichael

Một khi đã có n, chúng ta sẽ sử dụng hàm phi Carmichael:

λ(n) = lcm (p − 1, q − 1)

Phần này sẽ có thể hơi phức tạp. Bạn có thể bỏ qua và chỉ cần tin tưởng rằng phép toán hoạt động. Nếu không, hãy theo chúng tôi để thực hiện một vài phép tính khác. Mọi thứ sẽ được giải thích càng chi tiết càng tốt để giúp bạn nắm bắt những kiến thức cơ bản.

Đối với những người không biết, λ(n) là ký hiệu của hàm phi Carmichael, còn lcm là lowest common multiple (bội số chung nhỏ nhất) – nghĩa là số thấp nhất mà cả p và q có thể chia được. Có một số cách khác nhau để tìm ra điều này, nhưng cách dễ nhất là tin tưởng một máy tính online để làm phương trình cho bạn. Vì vậy, hãy đặt các con số của chúng ta vào phương trình:

  λ(701,111) = lcm (907 − 1, 773 − 1)

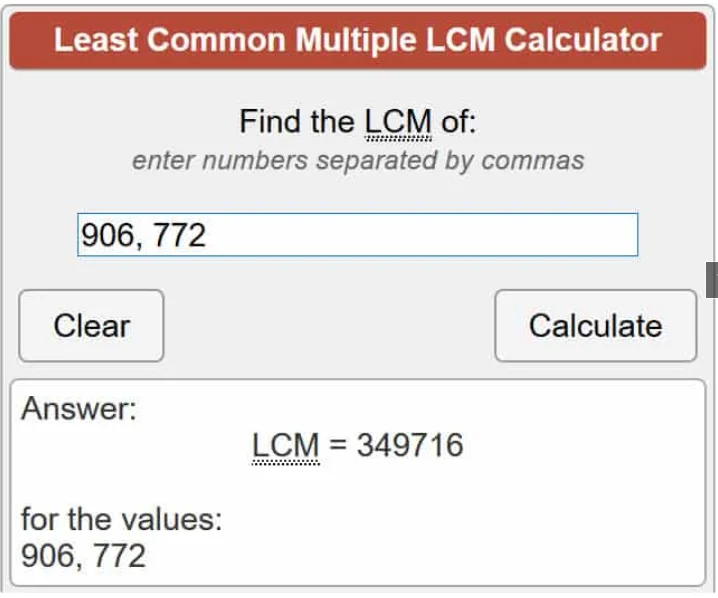
  λ(701,111) = lcm (906, 772)

Sử dụng máy tính chúng ta sẽ được:

 λ(701,111) = 349,716

 

Cách mã hóa RSA hoạt động trong thực tế

Các phần trên sẽ cung cấp cho bạn một hiểu biết hợp lý về cách thức hoạt động của phép toán đằng sau mã hóa public key nhưng nó có thể hơi khó hiểu. Trong các bước được liệt kê ở trên, chúng tôi đã chỉ ra cách hai người giao tiếp với nhau an toàn mà không cần chia sẻ mã trước đó. Đầu tiên, mỗi người cần thiết lập cặp key của riêng mình và chia sẻ public key với nhau. Hai người cần giữ bí mật về private key của họ để thông tin liên lạc của họ được bảo mật.

Khi người gửi có public key của người nhận, họ có thể sử dụng key đó để mã hóa dữ liệu mà họ muốn bảo mật. Khi nó đã được mã hóa bằng public key, nó chỉ có thể được giả mã bằng private key từ cùng một cặp key. Ngay cả cùng một public key cũng không thể được sử dụng để giải mã dữ liệu. Điều này là do các thuộc tính của chức năng hàm trapdoor mà đã được đề cập.

Khi người nhận nhận được tin nhắn được mã hóa, họ sử dụng private key của mình để truy cập dữ liệu. Nếu người nhân muốn gửi lại thông tin liên lạc theo cách an toàn, thì họ có thể mã hóa tin nhắn của mình bằng public key. Một lần nữa, khi nó đã được mã hóa bằng public key, cách duy nhất để thông tin có thể được truy cập là thông qua private key.

Theo cách này, mã hóa RSA có thể được sử dụng bởi các bên chưa biết trước đây để gửi dữ liệu một cách an toàn.